In post 23.4, we saw that the interpretation of x-ray diffraction patterns from crystals involves a temperature factor because atoms are displaced from their ideal lattice points by thermal vibrations. We have seen that heat is kinetic energy of atomic molecular motion (post 16.35). In a crystalline solid, the atoms must be oscillating about their positions in the equilibrium positions (post 22.21), otherwise it would melt (post 16.37). We saw, for the displacement of an atom that did not depend on direction, that we can allow for this effect by replacing the atomic scattering factor (the Fourier transform of an atom), f_j, by f_j’ where

f’_j = f_jexp(-K²σ_j²/2).                    (1)

Here K is the modulus of the vector that defines a position in K-space, and σ_j represents the standard deviation of all the positions of the atom. This result is usually written as

f’_j = exp(-B_j²sin²θ/λ²)                    (2)

where B_j is called the isotropic temperature factor for the atom, λ is the wavelength of the x-rays and sinθ is half the scattering angle (see appendix 2 post 23.2).

B_j is sometimes called the Debye-Waller factor. The Debye-Waller factor is named after the Dutch-American physicist Peter Debye (1894-1966) and Swedish physicist Ivar Waller (1898-1991). When the displacement of the atom is not the same in all directions, we need to replace the isotropic temperature factor by six anisotropic temperature factors.

I stated everything I’ve written so far in post 23.4 but without justification. The purpose of this post is to justify these statements.

Let’s start with isotropic vibrations and define the displacement, at any instant in time, from the position of the atom in an ideal crystal by u. The further the atom departs from this stable position, the greater its potential energy and the lower its kinetic energy. Since no external energy is supplied to the atom, it oscillates by exchanging potential and kinetic energy – it is a simple harmonic oscillator. If p₀ is the probability of finding the atom at its stable position and p_u is the probability of finding it at a given displaced position, then

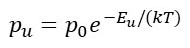
according to the Boltzmann distribution, where E_u is the increase in potential energy as a result of the displacement from the stable position, k is Boltzmann’s constant and T is the temperature on the Kelvin scale. If we define   q² = E_u   we can see that, p_u is given by   p₀ = exp(-aq²)   where   a = kT   is a constant at constant at constant temperature. According to post 24.1, p_u is now a Gaussian function so the distribution of atomic positions, about the stable position, is a Gaussian distribution (see post 24.1). Then

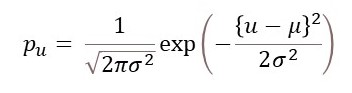
where μ is its mean position and σ its standard deviation. For an atom oscillating about its stable position,   μ = 0   so that

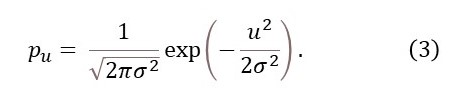
The position of the atom will be given by the convolution of its stable position and p_u as defined in equation 3.

Now let’s think about the contribution of this atom to x-ray diffraction by a crystal. X-rays scattered by a stationary atom can be represented, in amplitude and phase, by the Fourier transform of its electron density – the atomic scattering factor, f_j. When the position of the atom is described by a distribution function, like p_u, its position can be represented by the convolution of its stationary distribution with the distribution function (post 22.20). Then its Fourier transform is given by the Fourier transform of the stationary atom multiplied by the Fourier transform of p_u (post 22.20). Comparison of equation 1 of post 24.1 shows that the Fourier transform of p_u is given by

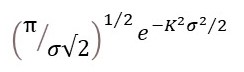
So that the Fourier transform of the oscillating atom is given by

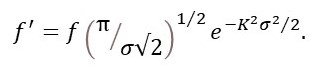
At constant temperature the total energy of the vibrating atom, and thus the standard deviation of its position, stays the same. Then the term in brackets is a constant that acts only as a scale factor, so f’ is given by equation 1.

It is conventional to define

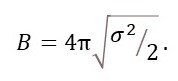
Noting that

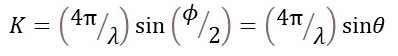
where ϕ is the scattering angle (post 22.23), you can calculate equation 2 from equation 1.

Now let’s think about anisotropic vibrations that are different in the different directions of the a, b and c unit cell vectors. The positions of the atoms are given by fractional unit cell coordinates, x, y and z, along these vectors. The position of an atom in an orthogonal Cartesian system is given by a vector. But the fractional unit cell coordinate system will not be orthogonal if the angles between a and b (γ), a and c (β) and b and c (α) are not 90^o. Then, for example, a displacement u along y will produce a displacement ucosα along z. So the position of an atom is not given by a vector because its components are not independent. It must be given by a tensor. Then B of equation 2 must be replaced by a tensor of the form

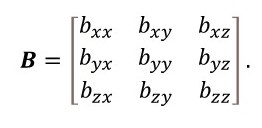
When i ≠ j, b_ij allows for the effect of a direction in one direction on the displacement along another direction. We have seen that a displacement u along y will produce a displacement ucosα along z. Similarly, a displacement w along z will produce a displacement vcosα along y. As a result, b_ij = b_ji (i ≠ j) and the only tensor elements values needed to needed to describe the anisotropic temperature factors are those shown in the matrix below.

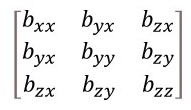
Look carefully and you will see there are only six anisotropic temperature factors (for example b_yx = b_yx and there is no need to use b_xy).

So we describe the thermal vibration of an atom in a crystal by one isotropic temperature factors or six anisotropic temperature factors.

Related posts

23.4 X-ray crystallography and molecular structure
24.1 Fourier transform of a Gaussian function