In post 18.6, we saw how the motion of a simple pendulum could be explained by it conserving mechanical energy. This explanation shows that the pendulum is an example of a simple harmonic oscillator – a system that does not dissipate mechanical energy and so continues to oscillate indefinitely. But this explanation involved a lot of mathematical manipulation. Because the idea of the simple harmonic oscillator is so important, I’m now going to explain the motion of the pendulum in a simpler way. We will then use the ideas, in later posts, to think about ideas like natural frequency and the control of motion.
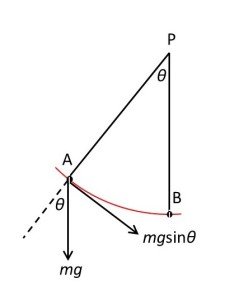
In the picture above, a small object of mass m hangs from a point P by a string of length L and negligible mass that cannot stretch. The object is moved to A (an angular displacement whose magnitude is θ, see post 17.39) and, when released, gravity makes it fall to B. When it falls, it moves along a circular arc (shown in red) because it is attached to P by a string of constant length.
Gravity pulls the object vertically downwards with a force of magnitude mg, where g is the magnitude of the earth’s gravitational field (post 16.16). The picture shows that the component of this force perpendicular to the string is mgsinθ (see post 16.50); the dotted line in the picture is the extension of the line PA. The torque that makes it move on a circular path is given by
T = – (mgsinθ)L
(see post 17.10). This torque is negative because it acts in a clockwise direction; the angular displacement, θ, is positive because it acts in an anti-clockwise direction (post 17.10).
According to post 17.39, the torque is also given by
T = I(d2θ/dt2) = mL2(d2θ/dt2)
where I is the rotational inertia which, for a particle of mass m a distance L from the axis of rotation, is given by mL2 (see post 17.38) and (d2θ/dt2) is the magnitude of the angular acceleration (post 17.39).
We now assume that the pendulum is a simple harmonic oscillator that conserves mechanical energy (post 16.21), just like a ball that continues to bounce perfectly elastically on a smooth horizontal surface (post 17.30). If the system conserves mechanical energy, there is no drag acting on the pendulum (post 17.17). Of course, no moving system is completely free from drag, so the simple harmonic oscillator is a model system that does not exactly describe any real system but helps us to understand how real systems behave – as discussed in post 18.6.
Since we have assumed that there is no drag, so no other forces are acting on the pendulum, the two expressions for T must be equal, so that
mL2(d2θ/dt2) = – (mgsinθ)L.
Dividing both sides of this equation by mL2 gives the result that
d2θ/dt2 = – (g/L)sinθ.
If the angular displacement θ is very small, sinθ is approximately equal to θ when it is measured in radians (post 17.11); this result is explained in the appendix. So, for small angular displacements, the equation above becomes
d2θ/dt2 = – (g/L)θ.
This equation is satisfied if
θ = cos(g/L)1/2t,
as explained in appendix 3 of post 18.6.

In post 16.50 we saw that the cosine of an angle repeats itself every 2π radians. We call the time in which the pendulum completes an oscillation, from A, through B to A’, in the picture above, and back to A, its time period T. Therefore,
2π = (g/L)1/2T so that T = 2π(L/g)1/2.
Since the frequency, f, of the pendulum (the number of oscillations it makes in unit time) is equal to 1/T (post 16.14), we can write that
f = (1/2π)(g/L)1/2.
This result it identical to that obtained in post 18.6, where we derived it from the principle of conservation of mechanical energy (post 16.21).
Note that A’ is the same height above B as is A. This is because, at both A and A’ all the mechanical energy of the system is potential energy. As A moves to B, this potential energy is converted to kinetic energy. At B all the mechanical energy is in the form of kinetic energy that is converted back into potential energy as the pendulum rises to A. Thus both A and A’ have the same potential energy and so are at the same height.
Related posts
18.6 The pendulum: a simple harmonic oscillator
17.13 Centripetal force
17.12 Going round in circles
17.11 Measuring angles
17.10 Torque
16.14 Aliasing
Follow-up posts
Appendix
The purpose of this appendix is to show that sinθ is approximately equal to θ measured in radians.
One way is to note that the series for sinθ, given in appendix 1 of post 18.6, converges very rapidly and so is approximately equal to its first term when θ is very small.

Another way is to use the picture above, in which the red curve is an arc if a circle of radius r. The black and green lines are radii of this circle and θ is the angle between them. If θ is measured in radians, the length of the red arc is rθ (see post 17.11). The blue line is perpendicular to the blue line, so that its length is rsinθ (post 16.50).
When θ is very small, the blue line and red arc are almost the same so that
rsinθ ≈ rθ or sinθ ≈ θ.