In posts 17.11 and 17.12 we saw that angular displacement, angular speed and angular acceleration can be defined, as vectors, in a way that is analogous to displacement, velocity and acceleration (post 17.4) along a line (not necessarily a straight line) in space – translational motion.

In post 16.12, we saw that translational motion could be explained in terms of mass, length and time. The table above shows how angular motion can be explained in an analogous way in terms of rotational inertia, angle and time. Although the analogy is exact, we must remember that our descriptions of rotational motion are also defined in terms of mass, length and time because rotational inertia is measured in kg.m² (post 17.38), angle is the number of times a length (the radius of a circle) fits into another length (the circumference of a circle) (see post 17.11) and time is the same for both types of motion. (If we measure angles in degrees instead of radians, the unit of angle is still a number – one revolution divided by 360).

The table above shows how we can use the fundamental concepts of the first table to define analogous concepts for both translational and rotational motion.

This paragraph shows how we can use these analogies. Let’s think about an object moving along a straight time. It starts with an initial speed of v₀ and has a constant acceleration of a. We can then derive (using the techniques of post 17.19) that the distance it moves, in time t, is given by

r = v₀t + ½at².

Now let’s think about an object moving around a circle. It starts with an initial angular speed ω₀ and has a constant angular acceleration of α. We can then use the analogy between translational and rotational motion to write, the equation

θ = ω₀t + ½αt²

without any further calculation.

However, you may notice that the definition of torque in the table is not the same as the definition in post 17.37. The definition in the table demonstrates the analogy between force (translational motion) and torque (angular motion); appendix 1 shows that this definition is equivalent to the one given previously.

In post 16.49, we saw that to stretch a spring from its resting length, by an increment ΔL, involved increasing the applied force from zero to F. We then defined the stiffness of the spring by

k = F/ΔL.

We used this result to derive that the work done to stretch the spring (and, therefore, the potential energy of the stretched spring) was given by

W = ½k(ΔL)².

Now that we have met the mathematical technique of integration (post 17.19), we can derive this result more neatly – as shown in appendix 2.

This definition and result applied to a spring that was stretched along a line. But some springs are spiral (see picture above). These spiral springs can be wound tighter by turning a handle. Before the work done to drive clocks and watches was provided by electricity from a battery, it came from the gradual uncoiling of a tightly wound spiral spring – the picture shows a spiral spring in a watch mechanism. Winding a spiral spring involves changing θ in the same way as stretching a conventional spring involves changing L. So, by analogy, we can define the stiffness of a spiral spring by

κ = T/Δθ

with the result that the wound spring can do work

W = ½κ(Δθ)².

Once the torsional stiffness, κ, has been defined, the rest follows by analogy.

Analogies like these enable us to use results derived for translational motion to write down the equations that govern rotational motion, and vice versa.

 

Related posts

17.38 Rotational inertia
17.37 More about torque – vector product
17.29 Centrifugal force
17.13 Centripetal force
17.12 Going round in circles
17.4 Displacement, velocity and acceleration

 

Appendix 1

1.1 Overview

The purpose of this appendix is to show that T = dL/dt.

In this blog, the definitions I give are not always the standard ones. I sometimes give an alternative definition, to make an idea easier to understand. But my definitions and the standard definitions are always equivalent.

In this appendix, I will derive the required result from the standard definitions but will show that these are equivalent to the definitions that I have given previously.

This appendix uses the concept of the cross product of two vectors (post 17.37).

1.2 To show that ω= r × v

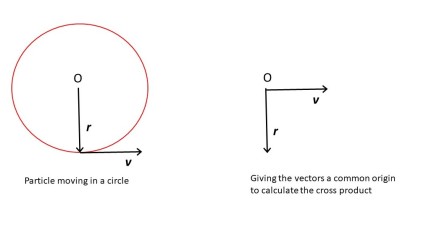
Think of a particle going round a circle of radius r with a velocity v. At an instant in time, the position of the particle is given by a vector r and v is perpendicular to r, in the plane of the circle (post 17.13 appendix 2). So r × v, in the picture, points towards you – in the same direction as the vector ω (post 17.12). By definition, the magnitude of this cross product is vr, which is the same as the magnitude of ω (post 17.12). So r × v has the same direction and magnitude as ω; this means that ω= r × v.

1.3 Definition of L and I

We can define L = r × p. This is analogous to the definition of T = r × F (post 17.37).

We use this definition of L to define I by the relationship L = Iω.

We need to be sure that this definition of I is the same as that introduced in post 17.38.

Think of a particle going round in a circle with a constant speed. Its kinetic energy (post 16.21) is given by

K = mv²/2 = p²/(2m).

We can think of this particle as rotating around an axis that passes through the centre of the circle and so can also write its kinetic energy as

K = L²/(2I) = (I²ω²)/(2I) = Iω²/2 = ½I(v/r)².

The two results are identical when I = mr², as in post 17.38.

1.4 To show that T = dL/dt

dL/dt = d(r × p)/dt = (dr/dt × p) + (r × dp/dt).

The final step is proved in appendix 3. Then

(dr/dt × p) + (r × dp/dt) = (v × p) + (r × dp/dt) = 0 + (r × F) = T.

(v × p) equals zero because the angle between p and v is zero.

 

Appendix 2

This appendix provides an alternative derivation of the work done in stretching a conventional spring (see the picture above). The general definition of the work done by a force is

For a spring of stiffness k, the stretching force is given by F = kx, where x is the extension of the spring (post 16.49). The integral then becomes

because F and x are in the same direction and ΔL represents the final extension. Evaluating this integral gives

Appendix 3

Here the values of u and w depend on the variable x but on no other variables; we say that they are functions of x only. An infinitesimal change in their product uw is given approximately by

δ(uw) ≈ (u + δu)(w + δw) – uw = uδw + δuδw + wδu.

Dividing both sides of this equation by the infinitessimal change in x that leads to the changes in u and w gives

δ(uw)/δx ≈ u(δw/δx) + (δuδw/δx) + w(δu/δx).

In the limit δx → 0 (post 17.4) δuδv becomes zero and we get the result that

d(uw)/dx = u(dw/dx) + w(du/dx).

In appendix 1.4, this result is applied to the cross product of two vectors.