The purpose of this post is to introduce three properties of the sphere that I hope to use in future posts. A sphere has a constant radius, R. The three properties that I want to explain are

1. Any radius of a sphere is perpendicular to its surface
2. The surface area of a sphere is 4πR²
3. The volume of a sphere is (4/3)πR³

The first might be difficult to understand – how can a line be perpendicular to a curved surface? To overcome this problem, I am going to define a tangent plane. A tangent plane touches the surface of the sphere at a point in the same way that a tangent of a circle is a line that touches its circumference at a point. Then we could consider the first property to be that any radius of a sphere is perpendicular to the tangent plane at which the radius meets the surface.

In the rest of this post, I am going to give proofs of these properties. So, if you are content to believe what you are told (and you probably know the second and third already) and/or don’t like mathematics, you can stop reading here.

A radius is perpendicular to the surface.

Any section of a sphere that contains its centre and a point on the surface, is a circle whose radius is a radius of the sphere. The tangent plane to the point on the surface appears in this section as a line that is a tangent to the circle.  In post 21.21, we saw that the radius of this circle is perpendicular to the tangent to the point at which the radius meets the circumference.

Since the tangent to the circle lies in the tangent plane and the radius of the circle is the same as the radius of the sphere, the radius of the sphere must be perpendicular to the tangent plane.

The surface area of a sphere is 4πR²

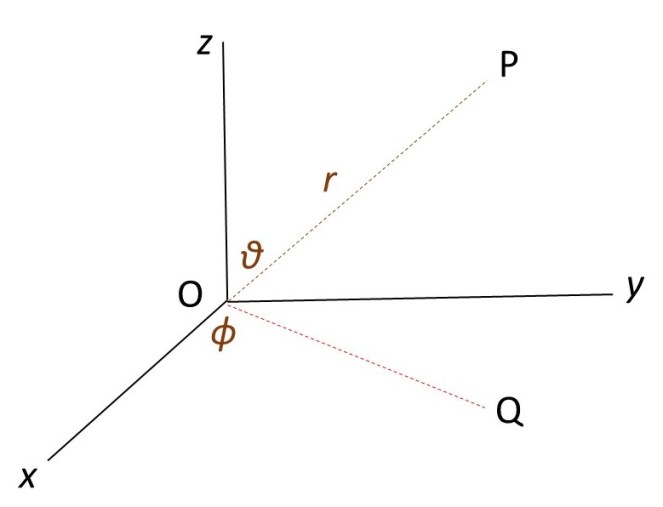
In this section, I am going to use spherical polar coordinates, described in post 22.15, whose origin, O, is at the centre of the sphere. Then a point P is specified by a distance, r, from O, and two angles, ϕ and θ, as shown in the picture above. This picture also shows the x, y and z-axes of an orthogonal Cartesian coordinate system whose origin is also at O; the line OQ lies in the xy plane.

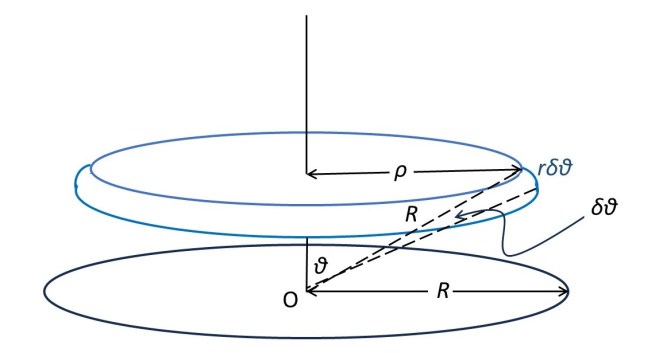
The picture above shows an elemental area of the sphere that is curved in two directions, like the sphere itself. Our need to describe this curvature of the spherical surface leads to the choice of spherical polar coordinates in this section. Our elemental area is defined by 0 < ϕ ≤ 2π and it subtends an angle δθ at O. Since δθ is infinitesimally small, we can consider the circumference and radius, ρ, and circumference, 2πρ, of our element at ρ and θ + δθ to be equal. The value of the circumference follows from the definition of π in post 17.11. The area of our elemental area is then its circumference multiplied by the arc length Rδθ; this result requires that we measure angles in radians throughout this post. So this elemental area is given by

δA = (2πρ).(Rδθ).

From the definition of the sine of an angle ρ = Rsinθ, so that

δA = (2πR²sinθ).(δθ).

Then the surface area of the sphere is given by the definite integral

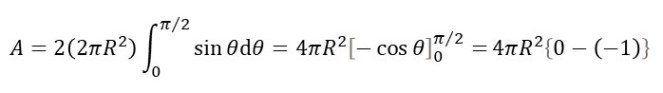
The factor of 2 arises because the limits of integration describe the hemisphere shown in the picture. So the surface area of the sphere is given by

V = 4πR².

The volume of a sphere is (4/3)πR³

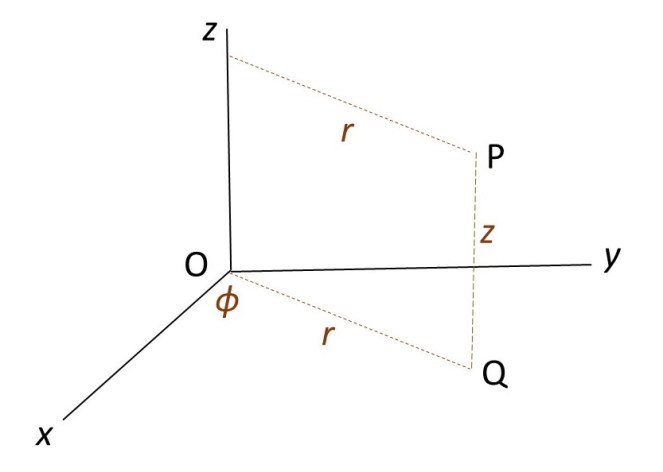
To derive this result, I’m going to think of the sphere as a stack of infinitesimal discs of thickness δz whose radius decreases from R, when z = 0, to 0, when z = R. To describe this stack of discs, I’m going to use a cylindrical polar coordinate system, origin at O, as described in post 24.12. In this system, we define the position of P by its perpendicular distance, r, from the z axis, an angle, ϕ, and a distance z, as shown in the picture below. In this picture, Q is the projection of P on to the xy plane of the Cartesian coordinate system that is also shown in the picture, so that OQ = r.

In this and the previous section, I am choosing a coordinate system that most simply describes the system I am analysing. The sphere has spherical symmetry and so I use a spherical polar coordinate system to describe an element of its surface that is curved in two directions. A stack of discs has cylindrical symmetry and so I use a cylindrical polar coordinate system. It is possible to analyse both systems using orthogonal Cartesian coordinates (this is how I was taught), or using the same polar coordinate system, but the mathematical manipulation involved is more difficult.

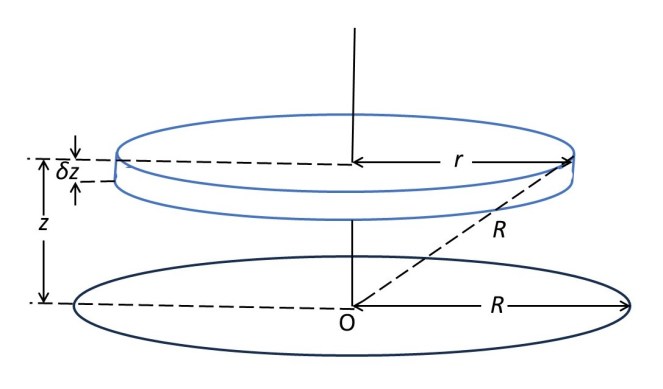
The picture above shows an elemental disc of thickness δz that is a slice of a hemisphere, radius R, that lies above the xy plane. Since δz is infinitesimal, we consider that the radii of its upper and lower surfaces to be equal to r so the area of the upper and lower circular surfaces of the disc is πr².(see the appendix). Then the volume of this disc is

δV = (πρ ²)δz.

In the picture, P, is on the circumference of the disc and, therefore, on the surface of the sphere; so the length of OP is R. By Pythagoras’ theorem

ρ² = R² – z²

so that

δV = π(R² – z²)δz.

Our hemisphere is defined by 0 ≤ z ≤ R, so the volume of the whole sphere is given by the definite integral

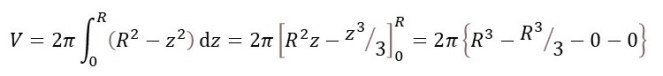
so that

V = (4/3)πR³.

Related posts

24.12 Atomic orbitals
22.15 X-ray scattering by an atom
22.8 The catenary
22.7 The caustic curve
22.6 Reflection at concave surfaces
21.6 The helix
21.5 Logarithmic spirals
21.3 Polar coordinates, circles and spirals
17.11 Measuring angles

Appendix

The purpose of this appendix is to show that the area of a circle of radius R is πR².

Consider the circle to consist of concentric rings. The radius of a ring is r and its thickness is δr. If  is infinitesimally small, the area of a ring is given by

δA = 2πr.δr.

Then the area of the circle is given by the definite integral

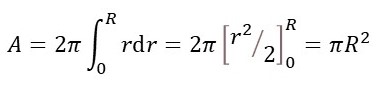
where R is the radius of the circle.