Before you read this, I suggest you read posts 16.30 and 24.12.

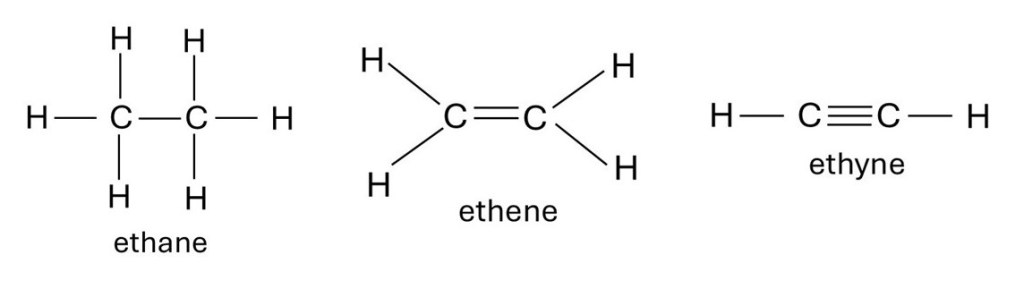
I am going to use the bonding in molecules of ethane, ethene and ethyne (see the picture above) to introduce the concept of hybrid orbitals. In post 16.31, we saw that, according to the valence bond theory, a molecule consists of atoms held together by chemical bonds; each bond is two electrons shared between two atoms in the molecule. The molecules I have chosen consist of two carbon atoms joined by a single bond (ethane), a double bond (ethene) or a triple bond (ethyne). Each carbon atom forms four bonds; in the four molecules the bonds that aren’t between carbon atoms are between carbon and hydrogen atoms, as shown in the picture above.

In post 24.12 we saw that the carbon atom has six electrons. Two of these electrons are in the low energy 1s orbital; because they are already paired with opposite electron spins (see post 24.12) they do not need to form bonds with other atoms (see post 16.30). The remaining four electrons are in 2s and the three 2p orbitals and we can represent the occupancy of electron energy levels in as 1s², 2s², 2p_x¹, 2p_y¹ (see post 24.12). If energy is provided to move an electron from 2s to 2p_z, the occupancy becomes 1s², 2s¹, 2p_x¹, 2p_y¹, 2p_z¹ and there are four unpaired electrons to form bonds as described in post 16.30.

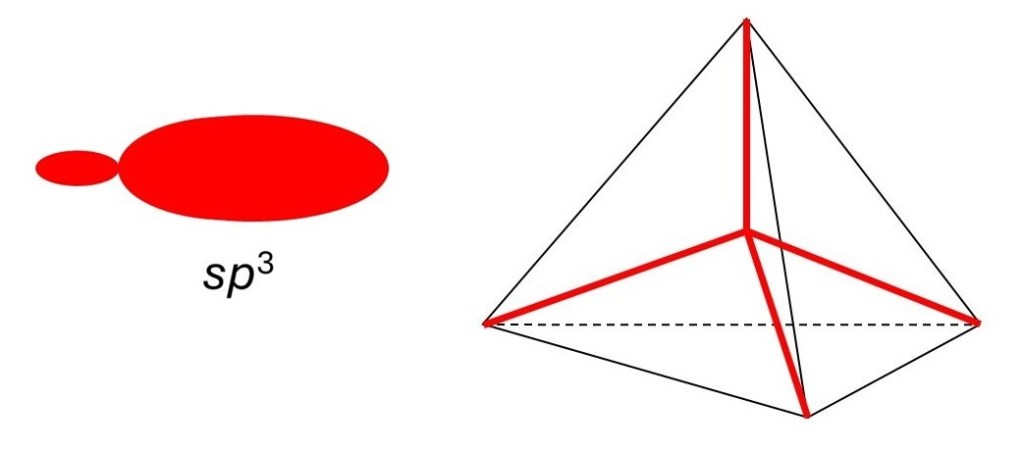
But in post 16.30 we saw that the four equivalent bonds in a molecule like methane, and similarly in ethane, point towards the corners of a tetrahedron because their electron pairs repel each other in a three-dimensional space. How can we reconcile this observation with the electrons in a carbon atom being in p orbitals that are mutually perpendicular (pointing along the axes of an orthogonal Cartesian coordinate system) and an s orbital that has no preferred direction? To answer this question, remember that the atomic orbitals are derived from wave functions that are solutions of Schrödinger’s equation – a partial differential equation. Remember also that any linear combination of solutions to a differential equation is also a solution (see post 19.10). So to explain the formation of four equivalent bonds in a molecule like methane we need to take a linear combination of the wave functions for the s, p_x, p_y and p_z orbitals to form four equivalent orbitals that point towards the corners of a tetrahedron. These four orbitals are called hybrid orbitals – because they are hybrids of the atomic orbitals used to describe the probabilistic positions of electrons in a free atom (see post 24.12). They are called sp³ orbitals and, because there are four of them that are equivalent in a three-dimensional space, they point towards the corners of a tetrahedron. Each sp³ orbital has a quarter of the character of an s orbital and three-quarters the character of a p orbital; one is shown in the picture below (left-hand side). The four sp³ orbitals are cylindrically symmetric about the red lines in the picture below (right-hand side). The angle between these red lines is about 109.5^o (see appendix 1). More details on the formation of sp³ hybrid orbitals is given in appendix 2.

The carbon atoms in ethene form bonds in three directions; each forms two single bonds with a hydrogen atom and a double bond with another carbon atom. So each carbon atom forms bonds in three directions. Since the electron pairs in these bonds repel each other, the three directions make an angle of 120^o with each other and define a plane; a brief explanation is given in post 16.47. Now let’s pursue this idea a bit further.

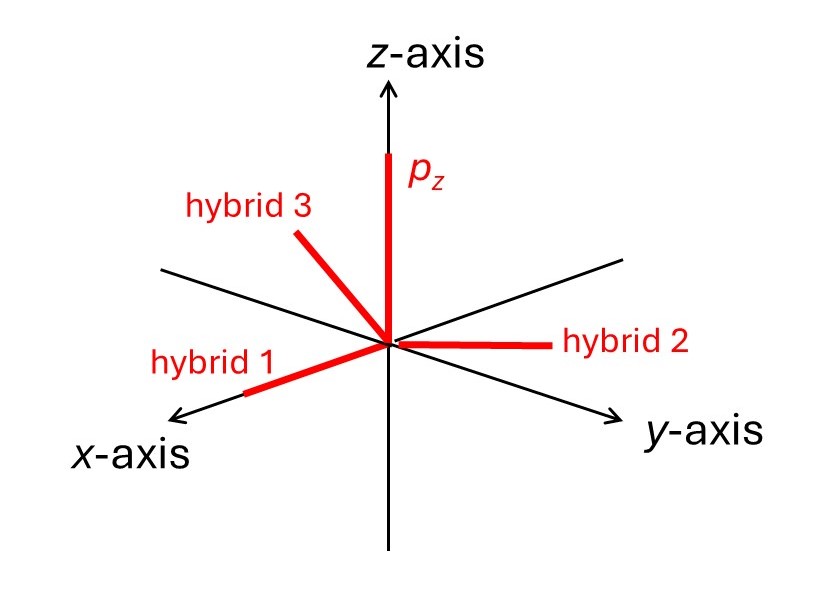
To form three equivalent bonds, we’ll start with a carbon atom with the electron configuration 1s², 2s¹, 2p_x¹, 2p_y¹, 2p_z¹, as we did before. But now we’ll take a linear combination of one s orbital and two p orbitals to form three equivalent sp² orbitals, each with one-third the character of an s orbital and two-thirds the character of a p orbital. So an sp² orbital is very similar to an sp³ orbital but a bit less elongated. Let’s take the p_x and p_y orbitals to make these hybrids, so that the electron configuration of our carbon atom can now be represented as 1s², 2(sp²₁)¹ 2(sp²₂)¹, 2(sp²₃)¹, 2p_z¹, where sp²₁, sp²₂ and sp²₃ represent three sp² hybrid orbitals that form an angle of 120^o with each other and the superscript 1 denotes the number of electrons in each orbital. The picture below shows the axes of the three hybrid orbitals (in red) lying in a plane (the xy plane) and making an angle of 120^o with each other and the p_z orbital perpendicular to the plane (in the z-direction); so the axes of the hybrid orbitals point towards the corners of an equilateral triangle. Since the three hybrid orbitals and the remaining p orbital contain a single, unpaired electron they can form chemical bonds. We will consider these bonds in more detail in the next post. More details on the formation of sp² hybrid orbitals are given in appendix 5.

The carbon atoms in ethyne form bonds in two directions; each forms a single bond with a hydrogen atom and a triple bond with another carbon atom. So each carbon atom forms bonds in two directions. Since the electron pairs in these bonds repel each other, the two directions make an angle of 180^o with each other and lie in a straight line. Now let’s think about forming the corresponding hybrid orbitals.

To form two equivalent bonds, we’ll start with a carbon atom with the electron configuration 1s², 2s¹, 2p_x¹, 2p_y¹, 2p_z¹, as we did before. Now we’ll take a linear combination of one s orbital and one p orbital to form two equivalent sp orbitals, each with half the character of an s orbital and half the character of a p orbital. So an sp orbital is very similar to an sp² orbital but is less elongated. Let’s use the p_x orbital and the s orbital to make the two sp hybrids, so that the p_y and p_z are not involved in hybrid orbital formation. The electron configuration of our carbon atom can now be represented as 1s², 2(sp₁)¹ 2(sp₂)¹, 2p_y¹, 2p_z¹, where sp₁ and sp₂ represent two sp hybrid orbitals that lie in a straight line (in the positive and negative x-directions). As before, the superscript 1 denotes the number of electrons in each orbital. Since the two hybrid orbitals and the two remaining p orbitals contain a single, unpaired electron they can form chemical bonds. In the next post, we shall see that the four atoms in an ethyne molecule then lie in a straight line. More details on the formation of sp hybrid orbitals are given in appendix 6.

Related posts

24.12 Atomic orbitals
16.31 Electrons in molecules
16.30 Molecules
16.29 Electrons in atoms

Appendix 1 The tetrahedral angle

The purpose of this appendix is to show that the angle between the red lines that join the centre of a regular tetrahedron to its corners (second picture in this post) is about 109.5^o.

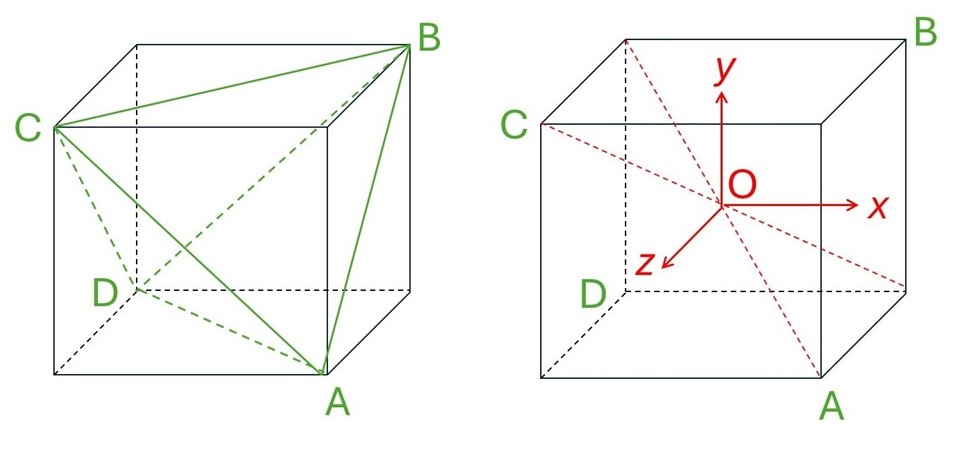
The picture above (left-hand side) shows the sides of a regular tetrahedron (shown in green) can be drawn by joining the corners A, B, D and C of a cube. The centre of the cube and, therefore, the centre of the tetrahedron, is at O in the picture above (right-hand side). I am going to define O as the origin of an orthogonal Cartesian coordinate system. The directions of the x, y and z-axes are defined by the sides of the cube and form a right-handed set as shown. If the cube has a side of length 2 units, the coordinate of A and B are (1, -1, 1) and (1, 1, -1), respectively. Then the vectors defining the positions of A and B are

a = i – j + k   and   b = i + j + k

(see post 17.3). The angle, θ, between these vectors can be calculated from their dot product defined as

a.b = abcosθ.

Calculating this dot product from a and b gives

a.b = 1 – 1 – 1 = -1.

The modulus of a and of b can be calculated from the dot products

a.a = 3   and   b.b = 3   so that   a² = 3   and b² = 3.

Then   a = √3   and   b = √3.

Substituting these values for a.b, a and b into the definition of the dot product gives the result that

cosθ = -1/3.

Using a calculator, arccos(-0.3333) is 109.47^o so that   θ = 109.47^o.

Appendix 2. Wave functions for sp³ hybrid orbitals

The wavefunctions for the four sp³ orbitals (ϕ₁, ϕ₂, ϕ₃, ϕ₄) are formed by linear combinations of the wavefunctions ψ_s (for the s orbital), ψ_x (for the p_x orbital), ψ_y (for the p_y orbital) and ψ_z (for the p_z orbital), so that

ϕ₁ = a₁ψ_s + b₁ψ_x + c₁ψ_y + d₁ψ_z                    1a

ϕ₂ = a₂ψ_s + b₂ψ_x + c₂ψ_y + d₂ψ_z                    1b

ϕ₃ = a₃ψ_s + b₃ψ_x + c₃ψ_y + d₃ψ_z                    1c

ϕ₄ = a₄ψ_s + b₄ψ_x + c₄ψ_y + d₄ψ_z                    1d

where a, b, c and d denote unknown coefficients whose values we need to determine.

Let’s start with the a coefficients. Since the s orbital is a sphere, it must contribute equally to all four hybrid orbitals. Since ψ_s will be normalised (that is it will have been subjected to normalisation), after solving Schrödinger’s equation , ψ_s² = 1. Then (a₁ψ_s)² makes a quarter of the contribution to ϕ₁² so that   (a₁ψ_s)² = ϕ₁²/4.   We want the wavefunctions for our hybrid orbitals to be normalised too, so that, for example, ϕ₁² = 1. Then    a₁²  = 1/4   or   a₁ = 1/2   . We can apply the same argument to all four hybrid orbitals with the result that

a₁ = a₂ = a₃ = a₄ = 1/2                   2

We can now start to determine the values of the other coefficients. We want the four hybrid orbitals to be independent of each other and not interact so they must be orthogonal (like the coordinates of a point in an orthogonal coordinate system) with the results that

a_na_m + b_nb_m + c_mcn + d_md_n = 0                    3

where   n = 1, 2, 3, 4   and   m = 1, 2, 3, 4   and   n ≠ m.   For more explanation, see appendix 3. And we want to ensure normalisation of their wavefunctions so that

a_n² + b_n² + c_n² + d_n² = 1                    4

as explained in appendix 4.

2.1 Coefficients in equation 1a

Now we are going to let the axis of ϕ₁ define the z-axis direction. Then b₁ = c₁ = 0 with the result that equation 1a becomes

ϕ₁ = a₁ψ_s + d₁ψ_z = (1/2)ψ_s + d₁ψ_z                   5

where the final step comes from equation 2.

From equation 4

1 = a₁² + b₁² + c₁² + d₁² =1/4 + 0 + 0 + d₁².

Then

d₁ = √3/2

So that equation 5 becomes

ϕ₁ = (1/2)ψ_s + (√3/2)ψ_z                   6

2.2 Coefficients in equation 1b

Now we are going to let the axis of ϕ₂ define the x-axis direction so that c₂ = 0 and equation 1b becomes

ϕ₂ = (1/2)ψ_s + b₂ψ_x + d₂ψ_z                   7

noting the value for a₂ from equation 2. From equation 3

a₁a₂ + b₁b₂ + c₁c₂ + d₁d₂ = 0.

Since b₁ = c₁ = 0 and substituting the results for d₁ from sub-section 2.1 gives

(1/2)(1/2) + 0 + 0 +(√3/2)d₂ = 0

so that

d₂ = -1/(2√3).

From equation 4

a₂² + b₂² + c₂² + d₂² = 1.

Substituting the values of the coefficients already obtained gives

(1/2)² + b₂² + 0 + {-1/(2√3)}² = 1/4 + b₂² + 1/12 = 0

so that

b₂ = √2/√3.

Now equation 7 becomes

ϕ₂ = (1/2)ψ_s + (√2/√3)ψ_x – (1/2√3)ψ_z                   8

2.3 Coefficients in equation 1c

Noting, from equation 3, that

a₂a₃ + b₂b₃ + c₂c₃ + d₂d₃ = 0

and the values of a₂ and c₂ in sub-section 2.2, gives

(1/2)a₃ + (√2/√3)b₃ + 0 + d₂d₃ = 0.

Remember that equation 2 establishes a value for a₃ so that this result becomes

(1/2)(1/2) + (√2/√3)b₃ + 0 + d₂d₃ = 0.                   (9)

Now we need to think geometrically. Think about a regular tetrahedron resting on one of its triangular faces as base. The origin of our hybrid orbitals is at the centre of this tetrahedron and their lobes point towards its corners. In sub-section 2.1, we defined ϕ₁ to point upwards in the positive z-direction. Then the lobes for ϕ₂, ϕ₃ and ϕ₄ must point in the negative z-direction by the same distance as each other so that

d₄ = d₃ = d₂ = -1/(2√3).

Now equation 9 becomes

(1/2)(1/2) + (√2/√3)b₃ + 0 + (1/2√3)(1/2√3) = 0

with the result that

b₃ = -1/√6.

From equation 4 (the normalisation condition)

a₃² + b₃² + c₃² + d₃² = 1

so that

(1/2)² + (1/√6)² + c₃² + (1/2√3)² = 1   or   c₃ = 1/√2.

Putting all the results from this sub-section into equation 1c gives

ϕ₃ = (1/2)ψ_s – (1/√6)ψ_x + (1/√2)ψ_y – (1/2√3)ψ_z.                    (10)

2.4 Coefficients in equation 1d

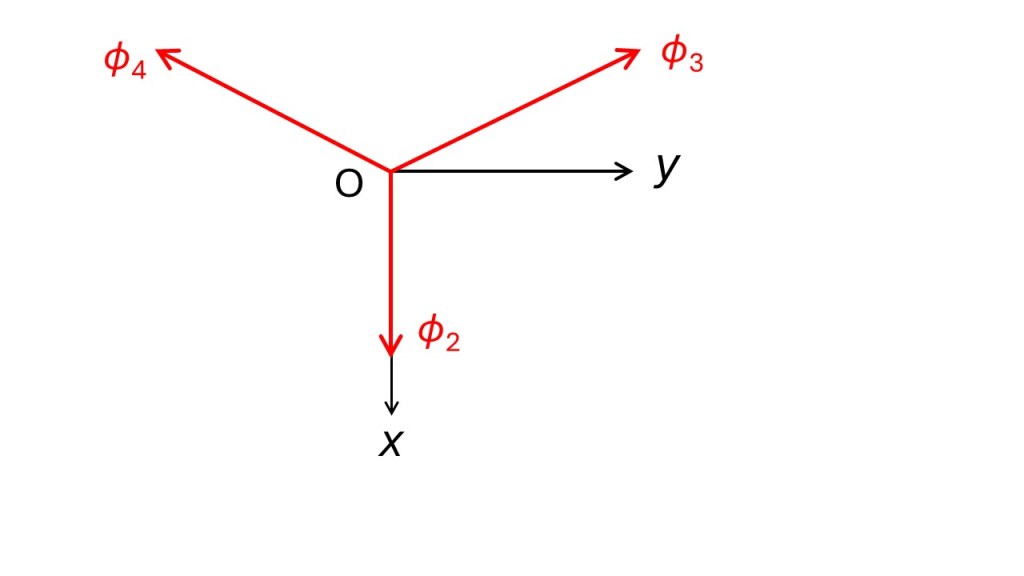
The picture above is a projection on to the xy-plane. The lobe of ϕ₁ points upwards, towards you, in the z-direction. The lobe of ϕ₂ lies in the xz plane and points away from you below the plane of the picture. I have defined the directions of the lobes of ϕ₂, ϕ₃, and ϕ₄ as the 2, 3 and 4 directions respectively. The angle between directions 2 and 3 is the same as that between 3 and 4 and between 4 and 2, because they are in the directions of the corners of a regular tetrahedron. For this to be true b₄ = b₃ (same coefficient for ψ_x) and c₄ = –c₃ (negate the coefficient for ψ_y). Otherwise the coefficients for are the same as in equation 10, so that equation 1d becomes

ϕ₄ = (1/2)ψ_s – (1/√6)ψ_x – (1/√2)ψ_y – (1/2√3)ψ_z.                    (11)

2.5 Angle between ϕ₁ and ϕ₂

I have chosen ϕ₁ and ϕ₂ as an example to show that the angle between the axes of sp³ hybrid orbitals is the tetrahedral angle of appendix 1.

I am going to represent the wavefunctions by vectors, as explained in appendix 3. From equation 6

ϕ₁ = (1/2)ψ_s + (√3/2)ψ_z

so that

r₁ = (√3/2)k

and its modulus

r₁ = (√3/2).

In representing ϕ₁ by r₁, we note that there is no specific direction associated with ψ_s.

From equation 8

ϕ₂ = (1/2)ψ_s + (√2/√3)ψ_x – (1/2√3)ψ_z

so that

r₂ = (√2/√3)i – (1/2√3)k

and

r₂² = (√2/√3)² + (-1/2√3)²   or   r₂ = √3/2.

Calculating the dot product of r₁ and r₂ gives

r₁.r₂ = (√3/2)(-1/2√3) = -1/4.

From the definition of the dot product

r₁.r₂ = r₁r₂cosθ = (√3/2)(√3/2)cosθ = (3/4)cosθ.

Comparing these results gives

(3/4)cosθ = -1/4   or   cosθ = -1/3

which is the tetrahedral angle of appendix 1.

Appendix 3 Orthogonality

In this appendix, I’m going to use the representation of a wave by a vector to explain equation 3.

In the picture above, the point P rotates about O, the origin of a two-dimensional orthogonal Cartesian coordinate system, with an angular speed ω so that, after time t, OP makes an angle ωt with the x-axis.

We can represent the position of P by the vector

r = ixcosωt + jrsinωt,

where i and j are unit vectors defining the x and y-axis directions.

We can also represent the position of P by the complex number

ψ = re^iωt

where r is the length of OP and i is the square root of -1. In post 18.11, we saw that the second representation can also be used to represent a wave of amplitude r and angular frequency ω.

So we can also use a vector to represent a wave.

Now let’s think about two three-dimensional vectors r₁ and r₂ defined by

r₁ = a₁i + b₁j + c₁k   and   r₂ = a₂i + b₂j + c₂k.

We can represent the dot product of the two vectors by

r₁. r₂ = a₁a₂ + b₁b₂ + c₁c₂

and could continue this property of the dot product into four or more dimensions.

We can also represent the dot product as

r₁. r₂ = r₁r₂cosθ.

If r₁ and r₂ are orthogonal, that is they are independent of each other, then θ = 90^o so that r₁. r₂ = 0. Then we can express the condition for orthogonality of r₁ and r₂ as

a₁a₂ + b₁b₂ + c₁c₂ = 0.

Applying this idea to our hybrid orbitals gives equation 3.

Appendix 4 Normalisation

In this appendix, I’m going to use the representation of a wave by a vector to explain equation 4.

In our vector representation, normalisation is ensuring that r_n. r_n = 1, so that

a_n² + b_n² + c_n² = 1.

For our hybrid orbitals we can extend this result to give equation 4.

Appendix 5. Wave functions for sp² hybrid orbitals

The wavefunctions for the three sp² orbitals (ϕ₁, ϕ₂, ϕ₃) are formed by linear combinations of the wavefunctions ψ_s (for the s orbital), ψ_x (for the p_x orbital) and ψ_y (for the p_y orbital), so that

ϕ₁ = a₁ψ_s + b₁ψ_x + c₁ψ_y                    12a

ϕ₂ = a₂ψ_s + b₂ψ_x + c₂ψ_y                    12b

ϕ₃ = a₃ψ_s + b₃ψ_x + c₃ψ_y                    12c

where a, b, and c denote unknown coefficients whose values we need to determine.

Since the s orbital is a sphere, it must contribute equally to all three hybrid orbitals. Since ψ_s will be normalised, after solving Schrödinger’s equation (see post 19.28), ψ_s² = 1. Then (a₁ψ_s)² makes a third of the contribution to ϕ₁² so that   (a₁ψ_s)² = ϕ₁²/3.   We want the wavefunctions for our hybrid orbitals to be normalised too, so that, for example, ϕ₁² = 1. Then    a₁²  = 1/3   or   a₁ = 1/√3   . We can apply the same argument to all three hybrid orbitals with the result that

a₁ = a₂ = a₃ = 1/√3.                   13

Let the x-axis define the axis of ϕ₁ then   c₁ = 0.

The condition for normalisation (appendix 4) is that

a₁² + b₁² + c₁² = 1.

Substituting values for a₁ and c₁ into this condition gives

(1/√3)² + b₁² + 0 = 1   so that   b₁ = √(2/3).                   14

The condition for orthogonality of our hybrid orbitals (appendix 3) is that

a₁a₂ + b₁b₂ + c₁c₂ = 0

and, since c₁ = 0,

a₁a₂ + b₁b₂ = 0.                    15

Similarly

a₁a₃ + b₁b₃ = 0.                    16

From equations 13, 14 and 15

(1/√3)(1/√3) + (√2/√3)b₂ = 0

so that

b₂ = -1/(√3.√2) = -1/√6.                 17

Again using the condition for normality gives

a₂² + b₂² + c₂² = 1.

Substituting from equations 13 and 17, for values of a₂ and b₂, into this result gives

(1/√3)² + (-1/√6)² + c₂² = 1   or   c₂² = 1/2   or   c₂ = ±1/√2.                    18

In the same way, from equations 13, 14 and 16 (instead of 13, 14 and 15) we could get the results that

b₃ = = -1/√6   and   c₃ = ±1/√2.

It might look as if a₂ = a₃, b₂ = b₃ and c₂ = c₃ which would make equations 12b and 12c identical. This makes no sense if we want to describe three different sp² orbitals. We can resolve this problem by choosing the positive square root for c₂, from equation 18, and the negative square root for c₃. Then equation 12 becomes

ϕ₁ = (1/√3)ψ_s + (√2/√3)ψ_x                                     19a

ϕ₂ = (1/√3)ψ_s – (1/√6)ψ_x + (1/√2)ψ_y                    19b

ϕ₃ = (1/√3)ψ_s – (1/√6)ψ_x – (1/√2)ψ_y                    19c

I am going to use equations 19a and 19b to show that the angle between the axes of sp² hybrid orbitals is 120^o.

Representing the wavefunctions by vectors (appendix 3) gives

r₁ = (√2/√3)i   modulus   r₁ = (√2/√3)

r₂ = -(1/√6)i + (1/√2)j = -(1/√2)(1/√3)i + (1/√2)j

so that its modulus is given by

r₂² = (1/6) + (1/2) = 2/3   or   r₂ = √2/√3.

Calculating the do product of r₁ and r₂ gives

r₁. r₂ = -(√2/√3).(1/√2)(1/√3) = -1/3.

From the definition of the dot product

r₁. r₂ = r₁r₂cosθ = (√2/√3)(√2/√3)cosθ = (2/3)cosθ.

where θ is the angle between the vectors. Comparing these results gives

cosθ = -1/2.

Using a calculator (arccos function) gives θ = 120^o.

(Alternatively, bisect an equilateral triangle to give two right-angled triangles and use the result to calculate cos60^o then use the expression for the cosine of the sum of angles, in the appendix to post 19.13, to find cos120^o).

Appendix 6. Wave functions for sp hybrid orbitals

The wavefunctions for the two sp orbitals (ϕ₁, ϕ₂,) are formed by linear combinations of the wavefunctions ψ_s (for the s orbital) and ψ_x so that

ϕ₁ = a₁ψ_s + b₁ψ_x                    20a

ϕ₂ = a₂ψ_s + b₂ψ_x                    20b

where a and b denote unknown coefficients whose values we need to determine.

Since the s orbital is a sphere, it must contribute equally to both hybrid orbitals. Since ψ_s will be normalised, after solving Schrödinger’s equation (see post 19.28), ψ_s² = 1. Then (a₁ψ_s)² makes a half of the contribution to ϕ₁² so that   (a₁ψ_s)² = ϕ₁²/2.   We want the wavefunctions for our hybrid orbitals to be normalised too, so that, for example, ϕ₁² = 1. Then    a₁²  = 1/2   or   a₁ = 1/√2   . We can apply the same argument to ϕ₂ with the result that

a₁ = a₂ = 1/√2.

The condition for normalisation (appendix 4) is that

a₁² + b₁² = 1   so that   (1/2) + b₁² = 1   or   b₁ = ±√(1/2).

The same argument would give an identical value for b₂. Using the positive square root for ϕ₁ and the negative square root for ϕ₂ gives, from equation 20, the wavefunctions become

ϕ₁ = (1/√2)ψ_s + (1/√2)ψ_x                    21a

ϕ₂ = (1/√2)ψ_s – (1/√2)ψ_x                    21b

Since the axes of ϕ₁ and ϕ₂ point along the positive and negative x-axis directions, respectively, the angle between them is 180^o.