Before you read this, I suggest you read post 25.9

I introduced the idea of a magnetic field in post 16.25 before I had written about vectors; I am returning to the topic now because I have written more about fields (posts 17.24 and 25.9) and about vectors (posts 17.2 and 17.3). A magnetic field is a field that exerts a force on a moving charge, that is it exerts a force on a conductor carrying a current; it does not exert a force on a stationary charge.

I will start with the magnetic field caused by a current, I, flowing in a long, straight wire, as in post 16.25. The direction of the current is defined by the unit vector i. I will define a position in space by a vector r, perpendicular to i so that r, the modulus of r, is a radius in a cylindrical polar coordinate system. A cylindrical polar coordinate system is useful here because the wire defines an axis about which we expect the results of the current to be cylindrically symmetric. We can define the magnetic field caused by this current as

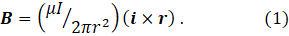
In equation 1, the direction of the cross product (i × r) defines the direction of B; μ is the permeability of the stuff surrounding the wire. To make this clear, let’s think about the mutually perpendicular unit vectors i, j and k that are used to define an orthogonal Cartesian coordinate system and define j to be in the r direction. It then follows that B is in the k direction, so that, given our definition of k (i, j and k form a right-handed set, as described in post 17.3 ), we could write

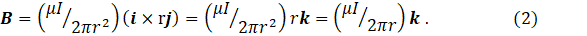
When I was at school, I was taught a rule (Fleming’s right-hand rule) to find the direction of B. But we don’t need it if we can do vector algebra. Equation 1 is a special case of the Biot-Savart law that we can use to define a magnetic field.

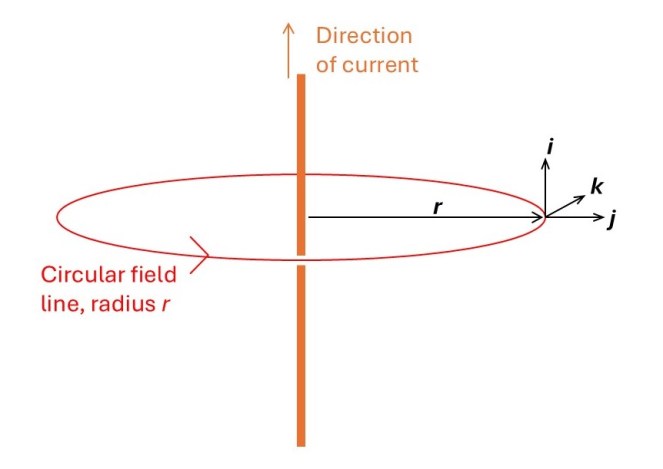
The picture above shows a magnetic field line defined by a single value of r. Since B is independent of the direction of r (equation 2), this field line is a circle of radius r, perpendicular to i and, hence, to the current in the wire that passes through the centre of the circle. As r increases, the field lines become further apart because B is inversely proportional to r.

We could equally well consider that a magnetic field is defined by the Lorentz law that describes its effect on a charge. This law has two parts (1) the force acting on a stationary charge (as the result of the electric field) and (2) the force acting on a moving charge (as a result of the magnetic field). If the moving charge is a steady current I₂ flowing in a length L of straight wire parallel to the wire that causes the field the second part of the Lorentz law becomes

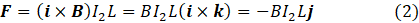
So the force on the conductor is in the negative j direction and so decreases with increasing r: so the field attracts the conductor towards it. The Lorentz law is named after the Dutch physicist Hendrik Lorentz (1853-1928).

From equation 2, we would expect the units used to measure magnetic field strength would be   (newton.amp^-1,m^-1)   that we could simplify as   (kg.m.s^-1).amp^-1.m^-1   or   kg.s^-1.amp^-1 (see post 17.41 for background information). But this unit has a special name – the tesla (abbreviated T) after the electrical engineer Nikola Tesla (1856-1943) who was born in Austria but settled later in the USA. Similarly, you might expect to measure magnetic flux in T.m² but this unit also has a special name – the weber (abbreviated to Wb), after the German physicist Wilhelm Weber (1804-1891).

In this post, I have concentrated on the magnetic field around a straight conducting wire. But fields around wires bent into other shapes are very important – the subject of a future post.

Related posts

25.17 Force on a current
25.16 Biot-Savart law
25.15 Magnets
25.14 Electromagnetic induction and fields
25.13 Electromagnetic induction
25.9 More about fields
19.9 Electromagnetic waves
17.44 Amps, volts and ohms
17.24 Fields and vectors
16.25 Electrical charge