Before you read this, I suggest you read posts 18.1 and 25.6.

A buffer keeps the pH of a solution constant. Buffers are used in laboratory experiments and occur naturally in ecosystems and our bodies. A simple laboratory buffer consists of the sodium or potassium salt of a weak acid dissolved in that acid.

So how does this simple buffer work?

The sodium (or potassium) salt of our acid (HA) consists of sodium ions (Na⁺; or potassium ions K⁺) and an equal number of anions (A^–; see post 17.49). (Here the word salt means a compound derived from an acid by replacing H⁺ by another cation.) The acid consists of some hydrogen ions (H⁺), an equal number of anions (A^–) and many more molecules (HA). The concentration of HA molecules and the ions it can dissociate into (H⁺ and A^–) is given by

K_a =[H⁺][A^–]/[HA]

where [square brackets] denote molar concentration (concentration measured in moles per litre) and K_a is a constant called the acid dissociation constant).

What happens when you try to decrease the pH of the solutions? You do this by adding H⁺ ions. But this is automatically followed by the extra H⁺ ions combining with A^– ions (mostly provided by the sodium or potassium salt) to keep K_a constant. So the pH doesn’t change.

What happens when you try to increase the pH of the solutions? You do this by removing H⁺ ions; this is achieved by adding an alkali (see post 17.50). For example, if the alkali is sodium hydroxide (a mixture of equal numbers of Na⁺ and OH^– ions), H⁺ ions will be removed because they combine with OH^– ions to form a water (H₂O) molecule. But this is automatically followed by HA molecules dissociating to keep K_a constant so that the H⁺ ions removed are replaced. The result is that the pH doesn’t change.

How do we know how much of the salt and how much acid we need to mix to make our buffer? We use the Henderson-Hasselbach equation to get the result

[A^–]/[HA] = 10^{(pH – pKa)}

that is derived in the appendix. To use this equation, we assume that the dissociation of HA molecules is negligible – a reasonable assumption for a weak acid. Then [HA] is equal to the molar concentration of the acid and [A^–] is equal to the molar concentration of the salt.

As an example, suppose we want to maintain the pH = 7.00 with a buffer made from acetic acid and sodium acetate. Acetic acid K_a = 4.76. Then

[A^–]/[HA] = 10^{7.00 – 4.76} = 10^2.24 = 174.

(If you don’t understand why I haven’t given the result of this calculation as 173.78, see post 16.7.) So the molar concentration of sodium acetate must be 174 times the molar concentration of acetic acid in our buffer.

Dissolved carbon dioxide is one way of buffering our body fluids and the sea. In our bodies, carbon dioxide is a product of respiration – the series involved in using the chemical energy of fats and carbohydrates (see post 16.47). When carbon dioxide (CO₂) dissolves in water some of the molecules react with water molecules to form carbonic acid (H₂CO₃). Some of these carbonic acid molecules can dissociate to form bicarbonate (HCO₃^–; also called hydrogen carbonate) and H⁺ ions. Some of the bicarbonate ions can further dissociate into carbonate (CO₃^2-) and H⁺ ions, although this second dissociation is negligible in body fluids like blood. This series of chemical reactions can be represented by

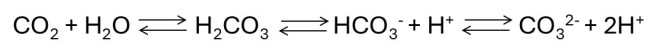
and the structures of the bicarbonate and carbonate ions are shown in the picture below. The double-headed arrows (red) and the curly arrows (blue) are explained in post 25.4; or ignore them and just look at the structures on the left-hand side of the picture.

The important part of this series of reactions for buffering our blood is shown below.

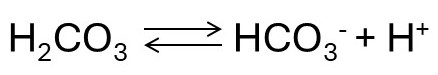
If anything happens that tends to acidify the blood, the additional H⁺ ions combine with bicarbonate ions to form carbonic acid molecules to because the value of K_a for carbonic acid must stay constant. And if anything happens to make the blood more alkaline, additional H⁺ ions are produced by the dissociation of carbonic acid molecules – for the same reason. This is also explained, in a slightly different way, in post 20.16. In this example the buffer consists simply of a weak acid (H₂CO₃) and its conjugate base (HCO₃^–); in our previous example the conjugate base was augmented by the sodium salt of the acid.

Sea water is buffered by the same reactions. But if the concentration of carbon dioxide becomes too high, the sea will contain excess carbonic acid molecules and hence excess H⁺ ions, so the pH of the sea decreases, that is the sea becomes more acid. This could be hazardous to some forms of marine life.

Related posts

25.6 Henderson-Hasselbach equation
25.5 Organic acids
20.16 Homeostasis 1
18.5 Calculating pH values
18.1 pH
17.50 Alkalis
17.49 Acids

Appendix

The Henderson-Hasselbach equation states that

pH = pK_a + log₁₀([A^–]/[HA]).

Here log₁₀(x) means the logarithm of x to the base 10 (see post 18.3). Rearranging this equation gives

log₁₀([A^–]/[HA]) = pH – pK_a

so the ratio [A^–] to [HA] to achieve our required pH is given by

[A^–]/[HA] = 10^{(pH – pKa)}.

This result follows from the definition of a logarithm (see post 18.3).