Before you read this, I suggest you read posts 17.49 and 18.3.

The extent to which an acid molecule, that I’ll represent as HA, dissociates to give a hydrogen ion (H⁺) and a cation (A^–) depends on its pK_a value and the pH of the surrounding solution. We can deduce this statement directly from the definitions of pK_a, pH and the acid dissociation constant.

However, the Henderson-Hasselbach equation states the relationship directly and makes it easy to use. The equation is named after the American chemist Lawrence Henderson (1878-1942) and the Danish chemist Karl Hasselbach (1874-1962). In this post, I will derive the equation and consider some of its applications.

In this paragraph, I use the convention that [square] brackets denote the molarity of a solution, that is concentration measured in moles per dm³ (see post 17.48). Remember that the acid dissociation constant is defined as

K_a = [H⁺][A^–]/[HA]

(see post 17.49) and taking logarithms (to the base 10; see post 18.3) of both sides of this equation gives

log₁₀K_a = log₁₀ [H⁺] + log₁₀[A^–] – log₁₀[HA].

(To understand this, and further, steps in the derivation, you may want to look at post 18.3). Rearranging this result gives

– log₁₀ [H⁺] = – log₁₀K_a + log₁₀([A^–]/[HA]).

From the definitions of pH and pK_a this gives

pH = pK_a + log₁₀([A^–]/[HA])

which is the Henderson-Hasselbach equation.

Notice that when the pH of a solution is equal to the pK_a of an acid that

log₁₀([A^–]/[HA]) = 0

so that

[A^–]/[HA] = 1.

This means that when pH = pK_a that half of the HA molecules are dissociated. We can use the Henderson-Hasselbach equation to deduce many relationships of this kind.

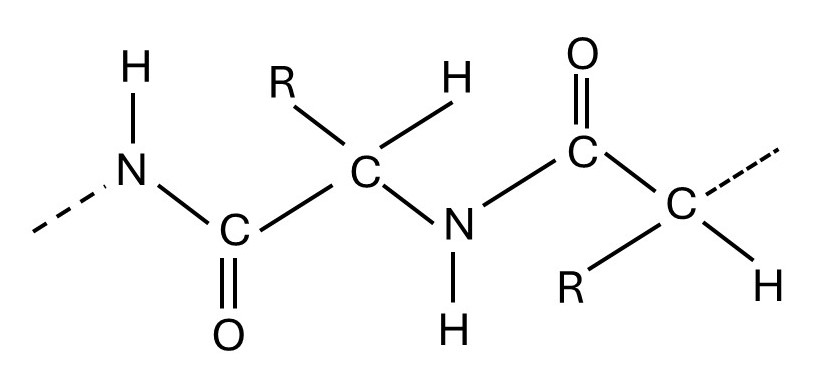
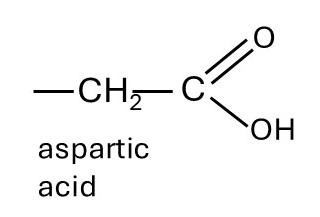
For example, I’m going to think about the amino acid side chains in protein molecules. The picture above shows two adjacent amino acid residues in a protein chain (see post 21.4). The R group depends on which amino acid occupies that position. The picture below shows R when the amino acid is aspartic acid. This R group has pK_a = 3.9 so that in a neutral solution (pH = 7.0)

log₁₀([A^–]/[HA]) = 7.0 – 3.9 = 3.1,

according to the Henderson-Hasselbach equation. Then

[A^–]/[HA] = 10^3.1 = 1.3 × 10³   or   [A^–] = 1.3 × 10³ × [HA].

This means that, at neutral pH, less than one in a thousand aspartic acid side chains has not dissociated so that almost all of them will have a negative charge. As a result, different aspartic acid residues in the same protein molecule will tend to repel each other and so influence how it folds in three dimensions.

The Henderson-Hasselbach equation is commonly used to calculate the pH of buffers – solutions that are used to control pH. I hope to write about this in my next post.

It also applies to alkalis as well as acids. An alkali is a base dissolved in water. A base (B) can react with water as shown by

B + H₂O → BH⁺ + OH^–.

Here BH⁺ is the conjugate acid of the base B. By analogy with K_a the strength of a base is defined by

K_b = [BH⁺][OH^–]/[B]

and

pK_b = -log₁₀K_b.

If we know the value of pK_b for B, we can calculate the value of pK_a for its conjugate acid from

pK_a + pK_b = 14

(see the appendix) and hence use the Henderson-Hasselbach equation in the same way as for an acid.

This post assumes that all the solutions are ideal. If this assumption is not valid, we need to replace the molar concentration by activity in all these equations and definitions.

Related posts

25.5 Organic acids
21.4 Proteins
18.5 Calculating pH values
18.1 pH
17.50 Alkalis
17.49 Acids

Follow-up posts

25.7 Buffers

Appendix

To show that pK_a + pK_b = 14.

We define the dissociation constant for water by

K_w = [H⁺][OH^–]/[H₂O] = 10^-14

(see post 18.5) so that

pK_w = -log₁₀K_w = -14.

Considering A^– as the conjugate base of HA gives

K_b = [HA][OH^–]/[A^–] = K_w/K_a = (10^-14)/K_a

so that

log₁₀K_b = -14 – log₁₀K_a.

Rearranging this result and noting the definitions of pK_a and pK_b gives

pK_a + pK_b = 14.