Before you read this, I suggest you read post 17.24.

In posts 16.25 and 17.24 I introduced the idea of a field as a region in space where something experiences force without being directly contacted by an object. In post 19.9 we saw that an electromagnetic wave is an electric and magnetic field that varies in time and space.

So, we can think of a field as a region in space and time where something experiences a force without being directly contacted by an object. There are other types of field, so this is really the definition of a force field. Since force is a vector, a force field is an example of a vector field. It is also possible to have a scalar field; for example, the number of electrons in an object is a scalar so that a function that represents the distribution of electrons in an object (see post 22.14) is an example of a scalar field. The mathematical definition of a field is more general. Here I have described a “field” as it’s usually used in physics.

To represent a vector field, we need to specify the direction of a vector at any point in space and time. We can do this by constructing field lines, also called lines of force. A field line is an arrow that points in the direction of the vector. The number of lines crossing a unit area at right angles represents the field strength. So the closer the field lines, the stronger the field.

For example, the gravitational field of an object of mass M at a point in space represented by a vector r, from its centre of mass, is given by

g = – GMu/r²

where r is the modulus of r, u is a unit vector in the direction of r and G is the gravitational constant. Remember that the centre of mass of a uniform sphere is at its geometric centre (see post 17.21). So the gravitational field lines for a sphere are represented by arrows pointing towards its centre because a gravitational field always attracts objects. The further we move from the surface of the sphere, the further apart the field lines become because the strength of the field is inversely proportional to the square of r.

Now let’s think about an electric charge, q. The electric field produced by this charge at a vector separation r is given by

E = qu/(4πεr²)

where r and u have the same meaning as before; ε represents the permittivity of the stuff surrounding the charge. So, if q is positive, the electrical field lines are arrows pointing away from it because it repels another positive charge.

When the modulus of a vector field is multiplied by an area perpendicular to the field, the result is called the flux. Let’s think about the electrical flux a distance r from q. The vector r, defines a sphere of radius r. The field lines are perpendicular to the surface of this field since the radii of a sphere are perpendicular to its surface (see post 25.8). The area of this spherical surface is 4πr² (see post 25.8) so the flux is

Φ = (4πr²)E = (4πr²)q/(4πεr²) = q/ε.

The idea of flux is simple when we are thinking about fields that are spherically symmetric. But in other circumstances it is more complicated. I will continue to use an electric field to explain the ideas but they apply to any vector field.

Let’s think about an elemental area δA. Now we will use u to represent a unit vector perpendicular to δA. If this elemental area is in a field E, then the flux across it is given by

δΦ = (E.u)δA

since the dot product E.u is the component of E perpendicular to δA. Since the component of a vector is a scalar, E.u is the modulus of the field perpendicular to δA. Now we define the flux to be the definite integral

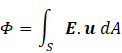
where the single (lower) limit, S, denotes integration over a whole surface. This is an example of a surface integral that we can think of as analogous to the line integral of post 17.36.

I intend to use the concepts of field lines and flux in posts that I want to write soon.

Related posts

25.14 Electromagnetic induction and fields
25.10 Magnetic fields
19.9 Electromagnetic waves
17.24 Fields and vectors
16.25 Electrical charge