Before you read this, I suggest you read post 25.2.
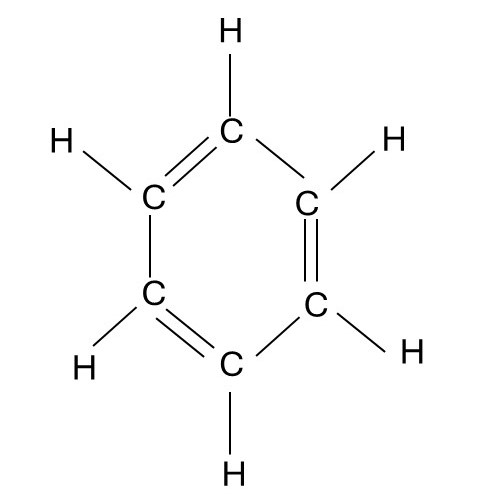
The formula of benzene is often written as shown in the picture above. The molecule shown here is a ring of six carbon atoms joined by alternating single and double covalent bonds. There is also a hydrogen atom bonded to each carbon atom. This structure was first proposed by the German chemist August Kekulé (1829-1896). (If you think his name appears to be French, it’s because his father changed it from the original German spelling of Kekule.)
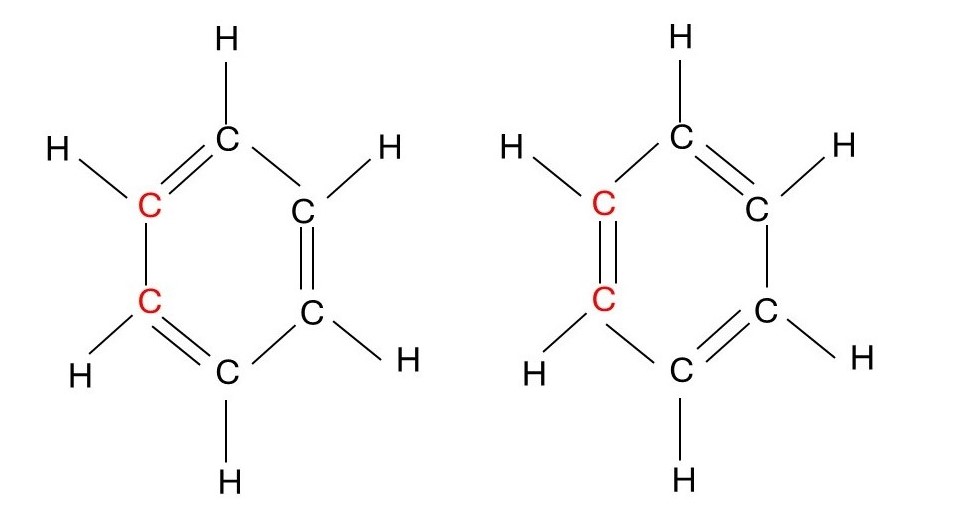
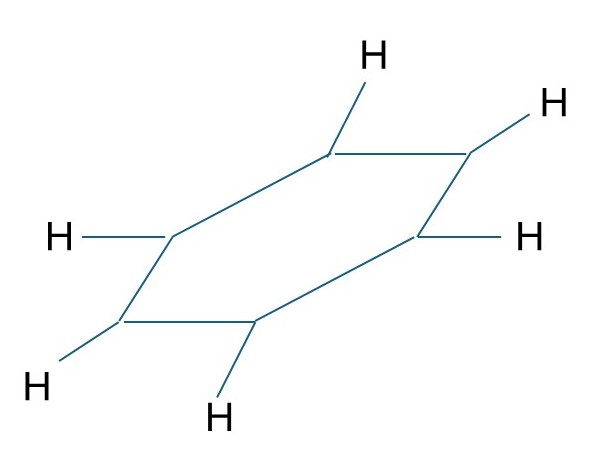
But how do we know which carbon atoms are joined by single bonds and which are joined by double bonds? This may look like a silly question because all carbon atoms are the same. But suppose two adjacent carbon atoms are the isotope C13, like the atoms shown in red in the picture above, and all the others are the usual isotope C12, shown in black. Now is the pattern of bonding the one on the right-hand side or the one on the left? To pursue this question, let’s use the valence bond theory to describe the structure of benzene, in the same way as we used it to describe ethene in post 25.2. We can consider that three of the four outer shell electrons in each carbon atom are each in a sp2 hybrid orbital and that the fourth is in a pz atomic orbital. The sp2 orbitals on adjacent carbon atoms, in the benzene ring overlap so that the atoms are joined by σ bonds. As a result, two sp2 orbitals from each carbon atom are involved in forming σ bonds with neighbouring carbon atoms. The third sp2 orbital forms a σ bond with a hydrogen atom, by overlapping with its s orbital. The result is the σ bonded framework shown in the picture below. I haven’t labelled the carbon atoms – they are at the junction of the bonds that form the six-membered ring. Since the sp2 orbitals lie in a plane all the atoms in the benzene molecule are in a plane.
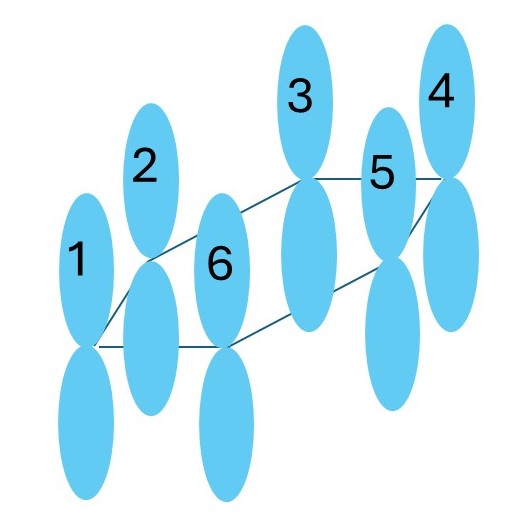
We now need to form a π bond by overlapping the pz orbitals that are perpendicular to the (xy) plane of the molecule. These pz orbitals are shown in the picture below. (I have omitted the hydrogen atoms to keep the picture simple.) But do we overlap orbitals 1 with 2, 3 with 4, and 5 with 6; or do we overlap 2 with 3, 4 with 5, and 6 with 1? We have no way of making a choice and the atoms have no way of choosing how to share their electrons. So we have a problem. One way to overcome it is to abandon the valence bond theory and describe the benzene molecule using the molecular orbital theory in which the electrons can be shared in delocalised π molecular orbitals (see post 16.31). We’ll return to this conclusion later. But first let’s look at some experimental evidence.
We can use x-ray crystallography to find the positions of atoms in molecules and so determine the lengths of bonds between atoms (see post 23.4). Benzene is a liquid, at room temperature, but many of its compounds are solids and their molecular structures have been determined by x-ray crystallography – an example is 1,3-dinitrobenzene (see picture below). The length of a C-C single bond is always about 0.15 pm and the length of a C=C double bond is always about 0.13 pm. But the lengths of the bonds between the carbon atoms in a benzene ring is about 0.14 pm. So the bond lengths between all the carbon atoms in the benzene ring are all equal and are mid-way between the lengths of a single bond and a double bond.
So now we have conceptual and experimental reasons for mistrusting the simple structural formula for benzene, based on the simple valence bond theory. So should we reject the valence bond theory and rely solely on the molecular orbital theory? Remember, also, that the molecular orbital theory could explain the paramagnetism of oxygen but the valence bond theory couldn’t (see post 16.31). But the valence bond theory is very useful. It provides a way of thinking about molecules as atoms joined together by discrete bonds. We can think of chemical reactions as a process of breaking old bonds and forming new ones. This gives chemists a way of planning how to make new molecules. It is especially useful in organic chemistry enabling chemists to plan how to make complicated new molecules, for example in drug discovery.
So we do what scientists usually do when a useful theory doesn’t work very well – we modify the theory, as I hope to describe in the next post.
Related posts
25.2 Sigma bonds and pi bonds
25.1 Hybrid orbitals
16.31 Electrons in molecules
16.30 Molecules
Follow-up posts