Before you read this, I suggest you read section 10 of post 22.10.

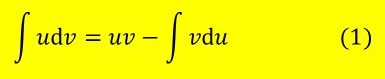
In post 22.10 we saw that integration reverses the process of differentiation. Suppose f and f’ are functions of x only and that

f’ = df/dx.                    (2)

To evaluate the integral

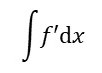
we recognise the function f that satisfies equation 2. Then

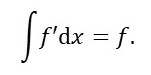
Sometimes this is easy but sometimes it isn’t. For example, in post 22.16, we saw that we sometimes need to use an operator called a Jacobian to evaluate an integral.

In this post I am going to explain another technique that I hope to use to evaluate integrals in my next post. This technique is called integration by parts and uses equation 1, highlighted in yellow, at the beginning of this post. In this equation u and v are functions of x only.

To prove equation 1, we start with the product rule

d(uv)/dx = u(dv/dx) + v(du/dx)

(see post 22.10) that can be rearranged to give

u(dv/dx) = d(uv)/dx – v(du/dx).

Integrating this result with respect to x gives

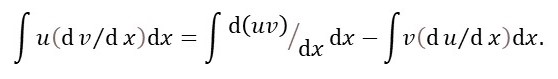
Evaluating these integrals gives

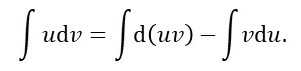
When we evaluate the first integral on the right-hand side of this equation, we get equation 1.

How do we use equation 1?

Let’s use it to evaluate the integral

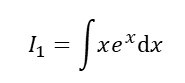
where e^x is defined (see post 18.15) by d(e^x)/dx = e^x. From this definition of e^x

Now let u = x and v = e^x. Then applying equation 1 gives

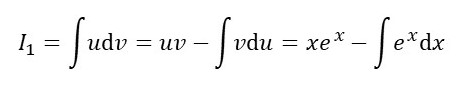
so that

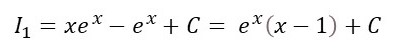
where C is a constant of integration.

We have evaluated I₁ using the technique of integration by parts.

Related posts

22.10 Differentiation
22.16 Jacobians