I have written about the discovery of electromagnetic induction by Faraday in post 18.21. This earlier post was about inductance in an electrical circuit. Now I want to concentrate on the phenomenon of induction itself. Like Heaviside, Faraday had never attended university but made many important discoveries in chemistry and physics working at the Royal Institution in London. Following his many discoveries, he was awarded an honorary doctorate by the University of Oxford; in 1991 his picture appeared on an English banknote. Unlike Heaviside, he knew very little mathematics but was able to explain his experimental results on induction by using the concept of field lines. Maxwell and Heaviside later expressed his ideas using more formal mathematics.

I am going to think about a closed loop of conducting material. This could be, for example, a length of copper wire whose ends are joined together. Faraday made two discoveries.

One: if he moved the loop in and out of a magnetic field (so that the magnetic flux, Φ_B, changed) an electrical current flowed in the loop.

Two: if the loop was stationary and the field changed (also changing the magnetic flux) a current also flowed in the loop.

Faraday noted that, in either case, the number of field lines passing through the loop changed. We can also think of the magnetic flux changing either because the coil moves in space (discovery one) or because the field changes with time (discovery 2).

The current flows because, in both cases, something provides energy to make charges flow in the loop (the charges are really electrons moving in the opposite direction – see post 17.44). This “something” is a source of energy usually called the electromotive force or emf and measured in volts. But it really isn’t a force. So I’m going to call it the induced voltage, V. Then V is the rate of change of Φ_B as time, t, changes. This result can be expressed mathematically as

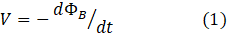
where magnetic flux is measured in webers and time is measured in seconds. This means is that the induced voltage is given by the change in the magnetic flux per second, when flux is measured in SI units.

Why is there a minus sign in equation 1? Remember that V dictates the direction in which the current flows – from a high value of V towards a lower value (see post 17.44). The induced current is associated with a magnetic field (see post 16.25) that I will call the induced magnetic field. When Φ_B increases, the induced field must decrease. If this were not the case, increasing the field would lead to it continuing to increase forever, violating the principle of the conservation of energy (the first law of thermodynamics). This result is called Lenz’s law and is the reason for the minus sign. A slightly different, but equivalent, explanation is given in post 18.21.

If you only want to know about the experimental results – stop reading here.

In post 16.25, we saw that a magnetic field exerted a force, F, on a charge, q, moving with a velocity v. The modulus of this force was given by F = Bqv,   where v is the speed, that is the modulus v. If we want to specify the direction of F, we can write this equation as

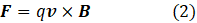
so that the direction of F is given by the direction of the cross product of v and B. Equation 2 is the magnetic term in the Lorentz law that I described in post 25.10. But I expressed the Lorentz law using the concept of current – it is usually expressed in terms of charge because it also includes the effect of the electric field – see appendix.

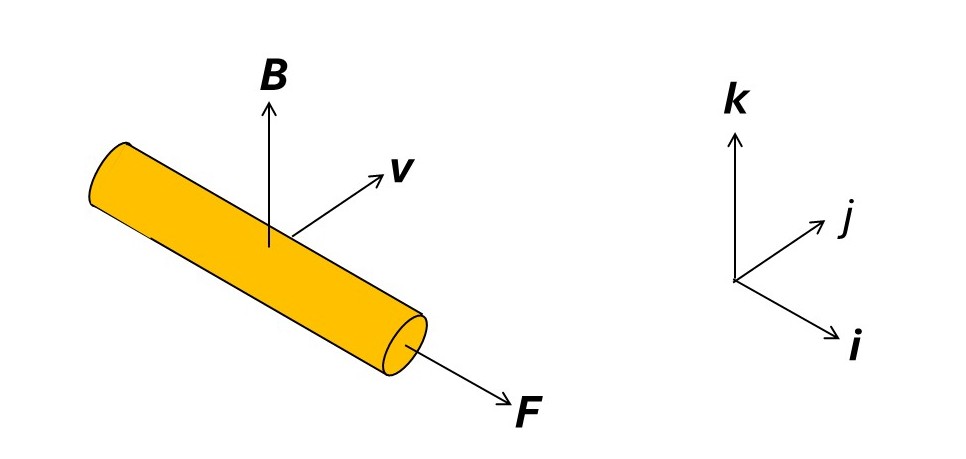
Now let’s think about moving a straight segment of a conductor, perpendicular to its length, with a velocity v perpendicular to a magnetic field, B. (as shown in the picture above). Let the direction of the segment (from left to right, in the picture) define the direction of the unit vector i, defining the x-axis of an orthogonal Cartesian coordinate system. Then v lies in the j direction (perpendicular to the segment). If the segment also moves perpendicular to B, then B lies in the k direction.

The segment is a conductor because it contains electrons that are free to move (see post 16.25). These electrons carry negative charge, so that moving the segment moves charges in the direction of v. According to equation 2, this creates a force, F, on the charges in the direction of j × k = i. This force moves the charges in the i direction to create a current (that is the free electrons move in the –i direction). So, movement of the segment moves charges in the j direction and this causes a simultaneous movement of charges in the i direction.

Related posts

25.14 Electromagnetic induction and fields
25.10 Magnetic fields
18.21 Inductors and inductance

Appendix

The Lorentz law also includes the effect of the electric field, E, and is

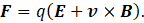
F is sometimes called the Lorentz force. The first term comes from the definition of an electric field and, from this post and post 25.10, the second term comes from the definition of a magnetic field.