Before you read this, I suggest you read posts 25.9 and 25.10.

Gauss’s law is a statement about the electric and magnetic flux in a defined volume of space. It is named after the German physicist and mathematician Carl Gauss (1777-1855). But a lot of other topics in mathematics and physics are named after him, including the Gaussian function, Gaussian distribution and Gaussian integral of post 24.1.

To understand Gauss’s law, it may help to think of the volume as being inside a closed container. But the container need not really exist – it can be completely in our imagination. If this seems crazy, think of a volume of space as being defined by a closed surface that need not be a physical boundary – I’ll call this closed surface a “container”.

I am going to explain Gauss’s law using the idea of field lines. But remember that field lines are only a way of helping us to think about the strength of a field – they are not some property of the field. Field lines represent the strength per unit area of a field. Now we’ll define the number of field lines, n, to be equal to the field strength (not simply proportional to the field strength).  Now the number, n, of field lines crossing a surface of area A is   n/A   and the flux   is, by definition, (n/A)A = n. This means that the number of field lines crossing a surface is equal to the flux crossing the surface.

Electric fields

Remember that an electric field has field lines whose origin is a charge.

Now let’s think about field lines from charges that are outside our container. Every field line that enters the container passes through it and comes out the other side. This means that the flux entering the container is equal to the flux leaving it. Charges outside the container have no influence on the flux inside the container.

Now let’s think about field lines from charges that are inside the container. A charge q is the source of flux q/ε, where ε is the permittivity of whatever is inside the container. (see post 25.9) If we consider that the container is completely empty (that is if it contains a vacuum) the flux is q/ε₀ where ε₀ is the permittivity of free space. If there are N charges,   q₁, q₂, q₃,……. q_i,…… q_N ,   inside the container, the total flux is the sum of the contributions from each of the charges and is

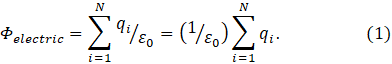
This result is expressed, in words, in the yellow box at the beginning of this post.

Magnetic fields

Magnetic field lines do not spread out from a point in space. As a result, the properties of magnetic flux are very different from the properties of electric flux. In post 25.10 we saw that magnetic field lines form a continuous loop. If we think of an elemental length of conducting wire, the current in this length creates a magnetic field whose field lines are concentric circles, surrounding the elemental length of wire. This will be true whatever shape the wire is bent into.

Now let’s think about our container that defines our volume of space. All the field lines that enter the container must leave it because they don’t begin and end anywhere. So the flux entering the container is equal to the flux leaving it – the total flux inside the container is zero. This result can be expressed as

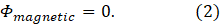
Equations 1 and 2 are Gauss’s law for electric and magnetic fields, respectively; they are explained, in words, in the yellow and green boxes at the beginning of this post.

Related posts

25.12 Differential form of Gauss’s law
25.10 Magnetic fields
25.9 More about fields
17.24 Fields and vectors